
Introduction
Optimization is the mathematical process that finds the best way to perform specific tasks. It involves finding the most efficient solutions to problems with specific constraints and objectives, such as determining optimal routes for transportation or scheduling production to minimize costs and maximize productivity. Some real-world examples of Optimization include estimating the minimum time to make a journey, minimizing the cost of doing tasks, reducing material usage used in engineering structures, or optimizing energy usage.
However, conventional optimization techniques such as Gradient Descent (GD) algorithms have limitations, such as computational resources, when solving complex multi-objective and multi-constraint optimization problems. Quantum-Inspired Evolutionary Algorithms (QIEA) are unmissable as they transform conventional optimization methods. With the unique ability to mirror the natural evolution process and leverage quantum computing principles, QIEAs are inspiring breakthroughs in various industries. This article explores how these algorithms are redefining Optimization and unlocking new possibilities for innovation.
The Challenges of Optimization
Computational complexity poses a significant challenge for optimization tasks. The Church-Turing thesis asserts that effective algorithmic solutions exist for any function, but the computational power and input size can affect the time required to solve the problem. Thus, an effective algorithm is crucial for computing and solving functions on any computing hardware, as emphasized by the Church-Turing thesis.
The capability of computers to compute any function depends on the availability of sufficient time and memory. However, the time taken to solve a problem is directly impacted by the machine's computational power and the size of the input data being processed.
Optimization problems, which often involve exhaustive searches, are closely associated with the P vs. NP-hard problem debate regarding efficient algorithms for solving them. Among many identified complexity classes, the P complexity class signifies problems recognizable in a polynomial amount of time, whereas NP stands for non-deterministic polynomial time, and algorithms can solve such issues as Optimization in exponential time with exhaustive search.
The Power of Gradient Descent Algorithms
Gradient Descent Optimization
(Source: Jiang, 2020)
The Gradient Descent algorithm has been widely used for optimization tasks, especially in machine learning applications. It can solve optimization problems effectively using a local search for minima if the function is smooth, locally continuous (holds Lipschitz continuity), comes in the intersections of PPAD (Polynomial Parity Argument on Directed Graphs) and PLS (Polynomial Local Search) class (GD = PPAD PLS) (FEARNLEY et al. 2022). As a result, it's primarily been used in modern machine learning applications. However, they struggle to find the global minimum for non-smooth optimization problems, leading to suboptimal solutions. Optimization in Engineering applications needs finding the best solutions that satisfy multiple conditions for achieving maximum efficiency and best performances. However, for multi-objective Optimization, it becomes computationally challenging.
Evolutionary Optimization: A Better Approach

Evolutionary Optimization
(Image Source: McCaffrey, 2012)
Evolutionary Optimization algorithms offer a promising alternative to Gradient Descent algorithms for complex optimization problems. Inspired by biological evolution, these algorithms can explore a more extensive solution space and find the global minimum faster [Tamilselvi, 2022].
"Evolutionary computation (EC) represents a class of heuristic optimization techniques inspired by biological evolution that may be used to solve challenging practical problems in engineering, the sciences." [Sofge, 2008].
The study demonstrates that even basic Evolutionary Algorithms (EA) exhibit significant competitiveness compared to advanced Gradient Descent algorithms, highlighting their advantage in solving specific types of computational problems, particularly in the Optimization field (Morse, 2016). They are particularly effective for solving NP problems classically. When optimizing multimodal objective functions with nonlinearities, interactions, and symmetries, classical Evolutionary algorithms face hurdles, get trapped in local minima, and may require significant computational resources to reach an optimal solution. Alternative algorithmic approaches are necessary to improve the efficiency of Optimization and enable practical application in real-world problems.
Quantum-Inspired Evolutionary Algorithms: A Quantum Leap in Optimization
Quantum-Inspired Evolutionary Algorithms (QIEA) bring quantum mechanical principles, such as superpositions and entanglement, into the realm of Optimization. These algorithms can leverage the power of both classical (near term) and quantum computing systems (mid-long term) to solve complex multi-objective and multi-constraint Optimization problems efficiently[Xiong et al. 2018]
QIEA's ability to obtain a large search solution space with a higher probability of finding the global optimum sets it apart from traditional optimization techniques. It surpasses Gradient Descent algorithms and applies to real-world engineering scenarios where multiple conditions with conflicting objectives must be optimized simultaneously.
Real-World Applications of QIEA

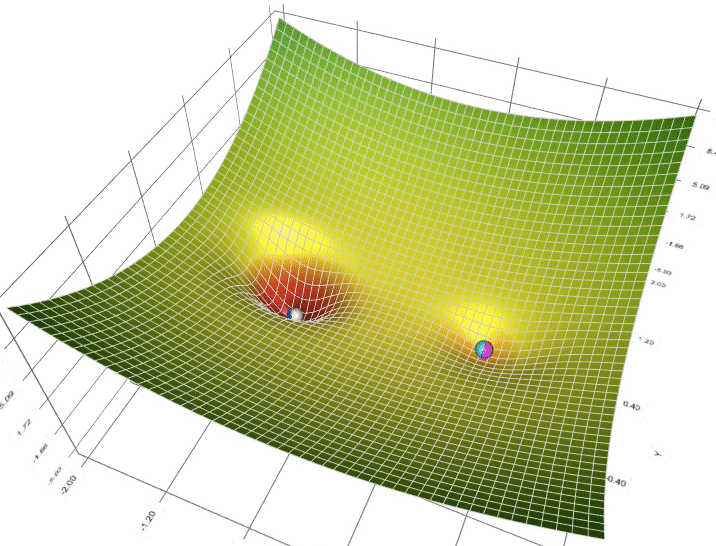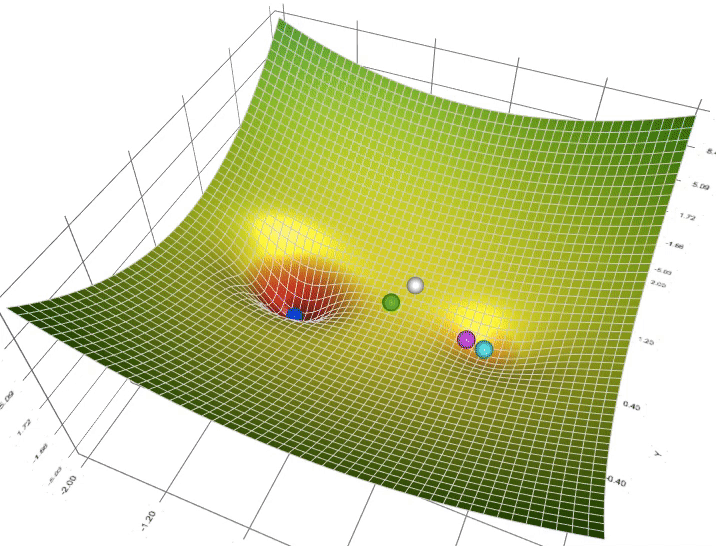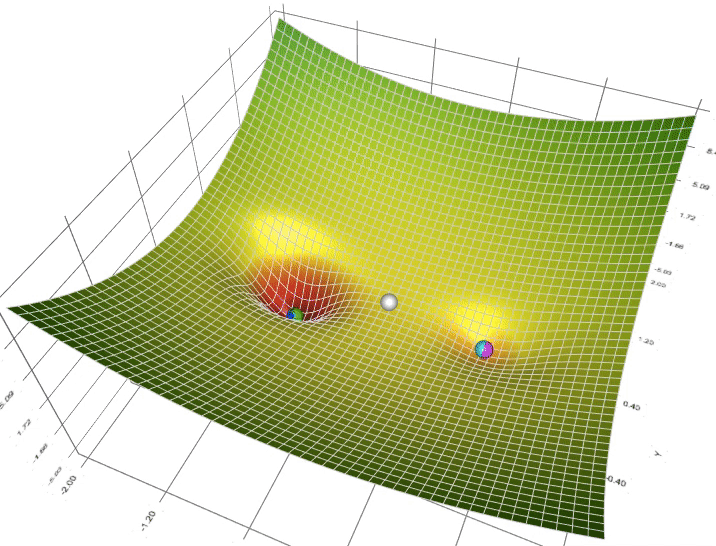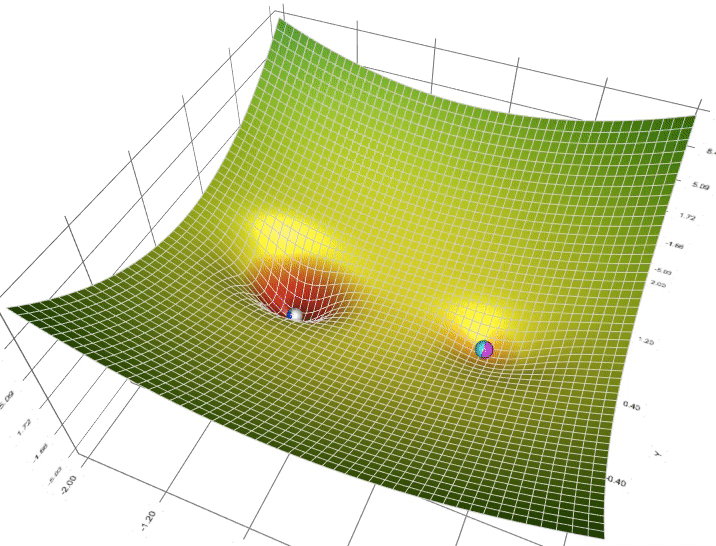
Figure: (Comparing BQPhy’s QIEO evolutionary vs. Classical Evolutionary approach, the optimal solution is obtained faster. This implies less computational resource is required to obtain the optimal result.)
BosonQ Psi has developed BQPhy®, a premium simulation software that utilizes QIEA to tackle complex engineering optimization problems. The QIEA-based design optimization solver (QIDO solver) in BQPhy® offers significant advantages over classical optimization approaches. With faster convergence and fewer iterations, it delivers more optimized engineering design solutions while requiring fewer computational resources.
BQPhy®'s QIDO solver has been successfully tested on various complex multi-objective and multi-constraint problems, including crash dynamics, weight optimization, and shape optimization. Its ability to explore a more extensive solution space and efficiently solve complex problems makes it ideal for engineering applications.
With BosonQ Psi's innovation in leveraging QIEA through the BQPhy® software, engineers can achieve faster, more optimized design solutions while conserving computational resources. Embracing the power of QIEA marks a quantum leap in Optimization.

